СМЕРШ
2 ранг
- Регистрация
- 30 Янв 2024
- Сообщения
- 1,530
- Реакции
- 1,450
- Репутация
- 56
- Страна
- Poland
- Город
- Stargard
- Предупреждений
- 13
- Что это такое и как с ним работать: https://kit-e.ru/switchercad-iii/
- Самое простое руководство по ЛТС. С него я и начинал: https://kit-e.ru/spice/
Почему ЛТС лучше всех симуляторов?
или:
Почему нет сверхлинейников ни в одном другом - да и быть не может?
Раз:
Корректность метода Ньютона зависит от (1) наличия непрерывных значений крутизны вольт-амперной характеристики каждого элемента схемы и (2) шунтирования всех нелинейных элементов конденсаторами так, что решение для предыдущей точки во времени является подходящей точкой для старта метода Ньютона для текущего временного значения.
Условия (1) и (2) встречаются в любой физической схеме, но программы, использующие SPICE, как правило, не умеют правильно их применять, потому что представление ВАХ полупроводниковых устройств в оригинальной реализации SPICE от Университета Беркли является дискретным. Это приводит к погрешностям, и такие ошибки реализации исходных моделей присутствуют изначально и в платных версиях SPICE.
В симуляторе LTspice такая дискретность отсутствует.
Для иллюстрации этих отличий на рис. 1 приведены вольт-амперные характеристики диода в PSpice по сравнению с их представлением в симуляторе LTspice. (PSpice является зарегистрированной торговой маркой компании Cadence. В приведенных иллюстрациях используется версия 9.2.).

Рис. 1.
а) Неравномерная вольт-амперная характеристика диода в PSpice;
б) равномерная вольт-амперная характеристика в LTspice. Неравномерности негативно влияют на способность симулятора моделировать нелинейные схемы.
Ваш симуль не покажет корректно искажения усилителя. Нельзя на его данных основывать свои схемотехнические решения: он - ледащо.
Два:
Интегральный метод Гира (Gear integration method) в PSpice часто выдает ошибочные результаты. Интегрирование по методу Гира подавляет не только числовые колебания, но и все колебания, включая физические. В результате схема некорректно функционирует в реальных условиях, так как симулятор показывает идеально стабильную работу модели, поскольку физические колебания некорректно демпфированы на этапе вычислений.
Уникальность LTspice заключается в том, что он использует самомодифицирующийся, самоассемблируемый и самолинкующийся код для вычисления разреженных матриц. Этот метод работает значительно лучше, чем другие технологии.
Это важно при расчёте устойчивости усилителя. Если ваш симулятор некорректно показывает будливую схему устойчивой, в железе усилителю однозначная торба.
Три:
*Метод Гира - неправильный перевод. ИМХО: шестерни, Gear.
Разработчики аналоговых схем считали, что интегрирование методом трапеций недопустимо для аналоговых схем (некоторые пользователи вынуждены с недоверием относиться к SPICE из-за популярной литературы, которая недооценивает значение симуляции в SPICE), поэтому оно было удалено из коммерческой версии реализации SPICE — PSpice, а как единственно доступный был оставлен более медленный и менее точный метод Гира.
Но интегрирование по методу Гира гасит не только числовые колебания, но и все колебания, включая физические. Данная особенность чревата тем, что схема некорректно работает в реальных условиях из-за присутствия колебаний, хотя симулятор показывает идеально стабильное функционирование модели.
Так происходит потому, что нестабильность схемы демпфирована на этапе вычислений. В результате возникали катастрофические ситуации, в которых интегральная микросхема, промоделированная и рассчитанная в PSpice, а затем изготовленная в промышленных масштабах, оказывалась неработоспособной. Впоследствии потребовались значительные временные и финансовые затраты для устранения этой нестабильности и достижения необходимой функциональности этой микросхемы.
Если разработчик микросхемы установит максимально короткий временной шаг, то в принципе ошибки интегрирования по методу Гира могут быть устранены. Но это не станет полноценным решением, поскольку (1) короткие временные шаги значительно уменьшают скорость симуляции и (2) нет никакого способа убедиться в том, что временной шаг действительно достаточно короткий.
В документации к симулятору PSpice указано, что он использует модифицированный метод Гира, который лучше справляется с задачей выбора действительно коротких временных шагов, чем реализация интегрирования по методу Гира в реализации SPICE от Университета Беркли.
Но метод, примененный в симуляторе PSpice, часто не работает. Очень просто создать обычную схему и увидеть, что численно интегрированный результат PSpice значительно отличается от реального решения, которое можно найти при расчете вручную. На рис. 2 показан параллельный резонансный контур с параллельно включенным источником тока. Источник тока выдает максимальный импульс тока в первые 0,2 мс, а затем падает до нуля. Решение предполагает, что резонансный контур возбуждается этим броском тока, а затем остается в режиме генерации с постоянной амплитудой.

Рис. 2. Простая схема с известным решением, выбранная для проверки
На рис. 3 показано, что модифицированное интегрирование методом Гира в PSpice искусственно гасит генерацию, в то время как симулятор LTspice выдает правильное решение с непрерывной генерацией вследствие отсутствия потерь в контуре.

Исходя из опыта автора статьи, модифицированный метод трапеций является лучшим средством для интегрирования дифференциальных уравнений для аналоговых схем, который не используется в других реализациях SPICE. Этот метод является единственным, который автор считает нужным рекомендовать для разработки схем.
На рис. 3 видно, что интегрирование по методу Гира в симуляторе PSpice некорректно объединяет две реактивные нагрузки в обычной схеме с одним узлом. В основе этих ошибок лежит то, что интегрирование по методу Гира пытается сделать схемы более стабильными в симуляции, чем они есть на самом деле. Чтобы показать практические последствия таких ошибок, на рис. 4 показан аудиоусилитель, нестабильно работающий потому, что величина емкости компенсационного конденсатора С2 слишком мала.

Рис. 4. Нестабильный усилитель мощности
PSpice некорректно моделирует данную схему как стабильную, в то время как симулятор LTspice демонстрирует верный результат.

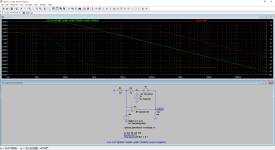
Рис. 5. Симуляция ответной реакции нестабильного усилителя мощности на большой скачок напряжения:
а) демонстрирует ошибочный стабильный результат;
б) показывает верный результат с наличием автоколебательного процесса от LTspice
На рис. 5 демонстрируется ошибочный стабильный результат (рис. 5а), а также верный результат с наличием автоколебательного процесса от LTspice (рис. 5б). На рис. 5 показана симуляция реакции на большой скачок напряжения. Если установить достаточно малый временной шаг симуляции в PSpicе, можно принудительно приблизиться к верному результату, допуская, что PSpice правильно интерпретирует уравнения моделей транзисторов и просто неточно интегрирует дифференциальные уравнения.
Модифицированный метод трапеций создан автором несколько лет назад и впервые стал широкодоступным в программе LTspice. Исходя из своего опыта, автор считает модифицированный метод трапеций, который не используется в других реализациях SPICE, лучшим средством для интегрирования дифференциальных уравнений для аналоговых схем.
Симулятор LTspice также поддерживает и другие методы, традиционный метод трапеций и метод Гира, однако они присутствуют в программе лишь для того, чтобы пользователь мог повторить ошибочные результаты из других реализаций симулятора SPICE и убедиться, что модели интерпретируются одинаково, но отличаются только методами интегрирования. (Ну, просто Бугога. Тролль ещё тот.))))
То есть: вы рассчитали в неком симуляторе свой усь, он опять сгорел.
Просто неправильный метод расчёта убедил вас, что усь устойчив,
а оказалось - это бочка с бензином.
Четыре:
Обратный пример: неправильный метод интегрирования видит звон там, где его нет.
На рис. 6 показана схема, которая создает паразитный «звон» из-за весьма высокой нелинейности емкости, вызванной нетрадиционно подключенными MOSFET-транзисторами в инверторе. «Звон» виден в источнике тока I(V1). На рис. 7 приведено сравнение традиционного метода трапеций и модифицированного метода трапеций, использованного в LTspice.


Рис. 7. Интегрирование методом трапеций по сравнению с модифицированным методом трапеций в LTspice (применительно к схеме, приведенной на рис. 6):
а) обычный метод интегрирования методом трапеций допускает появление «звона»;
б) интегрирование с использованием модифицированного метода трапеций в симуляторе LTspice полностью устраняет «звон»
Обратите внимание, что большинство реализаций SPICE не сможет запустить данную симуляцию, так как в них используется емкостная модель Мейера для этого типа MOSFET-транзисторов. Но поскольку емкостная модель Мейера не сохраняет заряд и выдает неточные результаты для коротких каналов, от нее отказались еще в 1990‑х годах.
Как в LTspice, так и в PSpice, емкостная модель Мейера (Meyer) заменена моделью заряда Янга — Чаттерджи (Yang — Chatterjee). В связи с тем что оба симулятора используют одни и те же обновленные уравнения сохранения зарядов, они должны выдавать и одинаковые результаты.
Но если мы сравним результаты в программах PSpice и LTspice, как показано на рис. 8, то увидим, что PSpice демонстрирует крайне ошибочные результаты. Колебания, наблюдаемые в PSpice, не дают «звона», потому что они не происходят на каждом временном интервале, а PSpice не использует метод трапеций.
Эти искажения практически полностью происходят вследствие ошибки дифференцирования уравнений Янга — Чаттерджи для емкостей, реализованных в модели зарядов в симуляторе PSpice.

Рис. 8.
а) Пример схемы, приведенный на рис. 6 в PSpice, не показывает «звон», но демонстрирует другие искажения, скорее всего из-за ошибки в применении модели заряда Янга — Чаттерджи;
б) симулятор LTspice дает корректный результат.
Заключение
LTSpice не первая и не единственная бесплатная реализация SPICE, но это самая лучшая и широко используемая реализация данного симулятора.Метод Ньютона, метод разреженных матриц и метод неявного интегрирования формируют ядро численных методов в SPICE. Надежность симулятора, его скорость работы и комплексность зависят от того, насколько хорошо эти методы реализованы.
Думается, симулятор LTspice вполне способен завоевать доверие разработчиков, наглядно продемонстрировав им свое умение корректно просчитывать поведение схем и выполнять важнейшие численные методы и делая это гораздо лучше других реализаций SPICE.
Автор:
Энгельгардт Майк (Engelhardt Mike)
Тут приведены цитатные отжимки, насколько возможно полно передающие суть.
Более подробно - тут:

SPICE Differentiation.Различия в реализациях симуляторов SPICE
Для прогнозирования работы электронных схем разработчики аналоговой техники часто опираются на результаты компьютерного моделирования. Ценность такого
Очень полезное руководство по симуляции трансформаторов.
Вложения
Последнее редактирование модератором: