А что это изменит? Синусоиды наотрез откажут складываться?
Сразу пример, чтобы были понятны подводные камни попыток без учета фазового спектра делать обобщения по одному лишь энергетическому спектру.
У одиночного коротко импульса энергетический спектр имеет примерно такой вид.
Обратите внимание, что его спектр не дискретный, а непрерывный. Другими словами энергия сигнала распределена по всему частотному диапазону, а не сосредоточена на нескольких отдельных частотах. Это характерно для недетерминированных сигналов, таких как случайный шум и переходные процессы. Заметьте, что, начиная с определенной частоты, уровень равен нулю. Эта частота обратно пропорциональна длительности импульса, поэтому чем короче импульс, тем шире его частотный состав. Если бы в природе существовал бесконечно короткий импульс (говоря математически, —
дельта-функция), то его спектр занимал бы весь частотный диапазон от 0 до +
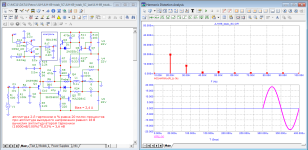
А у периодически повторяющегося во времени с некоторой частотой короткого импульса, энергетический спектр уже совсем другой.
Если импульс, имеющий приведенный выше спектр, повторяется с постоянной частотой, то результирующий спектр, который показан, здесь, будет уже не непрерывным, а состоящим из гармоник частоты повторения импульса, а его огибающая будет совпадать с формой спектра единичного импульса.
И по виду только одного энергетического спектра нельзя точно воссоздать временную форму самого сигнала, порождающего такой спектр. Вы не можете сказать, это сумма стационарных синусов или спектр импульсного сигнала. Вот в чем загвоздка.
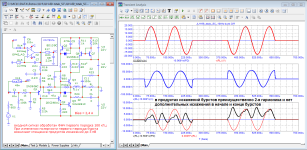
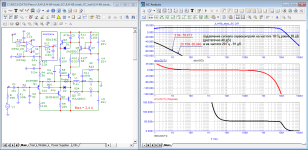
А для анализа искажающих свойств УНЧ (в том числе и динамических искажений в УНЧ, о которых, как я понял, была дискуссия выше), лучше использовать не стационарные сигналы типа одиночного синуса, пачки, заполненной синусом или даже суммы синусов на нескольких частотах (мультитона), а импульсные сигналы в виде периодически повторяющегося короткого импульса с некоторой частотой, например как на этой картинке
С таким спектром.
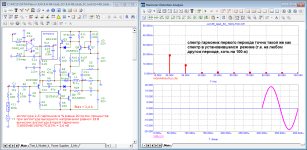
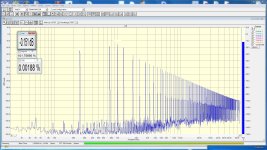
Анализ спектра такого импульсного сигнала покажет все возможные виды искажений в УНЧ и линейные и нелинейные и интермодуляционные и инерционно нелинейные искажения и динамические искажения. Может быть за исключением некоторых специфических, достаточно медленных инерционно-нелинейных искажений.
А еще информативней будет анализ импульсных сигналов в виде пачек сигналов с широким спектром. И тут уже лучше использовать не периодические повторяющиеся короткие импульсы, которые следуют относительно редко, с частотой повторения допустим в 30 Гц, чтобы охватить анализ всевозможных искажений и во временной и в частотной области на частотах от 30 Гц и выше. И энергетика которых получается небольшой.
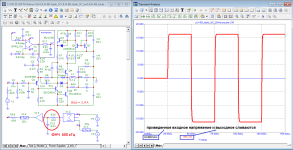
А пачки энергетически более мощных, импульсных сигналов, например в виде пачек меандров или пил с таким видом их спектров.
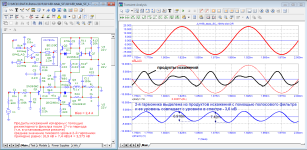
Причем, в подобных сигналах можно менять как частоту заполнения широкополосных сигналов, так и скважность и уровень самих пачек сигналов. В виду простоты формы таких сигналов и их большой схожести с реальными, импульсными, музыкальными сигналами, их очень просто анализировать визуально с помощью осциллографа - в меандре все углы должны быть максимально прямыми, а у пилы должен быть хотя бы один линейный участок (как во входном сигнале - оригинале). И любые виды искажений в УНЧ сразу приведут к заметному изменения и формы реализации сигнала на выходе УНЧ и его спектра. Тут, на мой взгляд, получается анализ "сразу все в одном" для интегральной или комплексной оценки качества или точности работы УНЧ, или, вообще, любой другой системы связи или передачи сообщений (вай-фая, блютуза, радиоканала и т.д.) по всем известным сейчас в науке видам искажений.

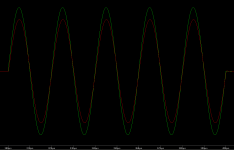
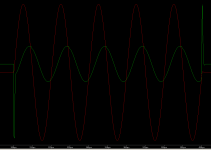

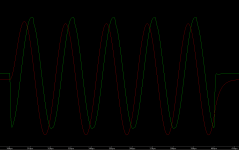






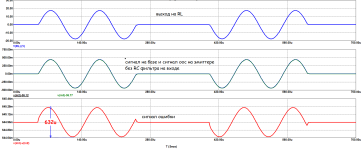










 Сможете его показать на графиках?
Сможете его показать на графиках?


