Цифровая обработка звуковых сигналов

[uriy]

Да кажись можно, есть два независимых проекта по коммутации при помощи ВАК (виртуальный аудио кабель). В одном проекте точно указана возможность через ASIO...

Как я понимаю сама суть асио это прямой эксклюзивный доступ одного софта к драйверу звуковой карты, и ни какой другой софт не может перехватывать соединение. Если между софтом и звуковой картой есть другой софт прокладка, то это уже не асио режим. Да и потом, асио нужно для реалтайма обработки звука т.е. получить минимальную задержку между звуком на выходе/ входе звуковой карты и софтом, а если применять АРО с КИХами то это всё преимущество накроется медным тазом т.к. КИХ имеет задержку.

 

[Freepainter]

Как я понимаю сама суть асио это прямой эксклюзивный доступ одного софта к драйверу звуковой карты, и ни какой другой софт не может перехватывать соединение. Если между софтом и звуковой картой есть другой софт прокладка, то это уже не асио режим. Да и потом, асио нужно для реалтайма обработки звука т.е. получить минимальную задержку между звуком на выходе/ входе звуковой карты и софтом, а если применять АРО с КИХами то это всё преимущество накроется медным тазом т.к. КИХ имеет задержку.

Так у асио тоже есть задержка. Я, так понимаю: если слушать музыку, то главное как она звучит, а какая там задержка не имеет значения. А вот, например, подключить муз. инструмент и что то играть в реальном времени, то задержка должна быть минимальна.
На FL Studio у меня задержка 4мкс и нет проблем в игре на эл.гитаре и записи...
Кроссовер высококачественный проще сделать в "железе" , я так и поступил и идеи с софтом давно оставил...
Вот еще одна ссыль на VAC с асио : http://jackaudio.org

 

[Rimtotal]

Да кажись можно, есть два независимых проекта по коммутации при помощи ВАК

Спасибо, с Virtual Audio Cable я уже имел знакомство, устанавливал настраивал, но не смог разобраться.
Доп каналы создал, как на каждый отдельный канал перед тем как он уходит на усилитель навесить VST плагин Fabfilter Pro-Q 3, что бы уже в нем настроить фильтр, разобраться не смог.
инструкции на просторах инета все о другом.

а если применять АРО с КИХами то это всё преимущество накроется медным тазом т.к. КИХ имеет задержку.

Задержки не так страшны для музыки, точнее наоборот полезны когда ими можно управлять.
а вот обойти системный микшер виндовса при помощи асио и не лишиться всех настроек АРО было бы здорово

 

[Freepainter]

Вот еще нашел у себя в архиве док. по настройке vac по первой ссылке, там в конце есть описание настройки кроссовера...
Фраза в конце: "...данные графики и идеальный импульс через виртуальный кабель идут бит в битик, по крайней мере REW при замере через него рисует идеальные" (с)!

 

[Zandy]

Юрий, спасибо за проверку.
А у меня тут родилась новая идея, пока только в голове (во время обеда). Попробую воплотить ее в схему вечерком, если время будет.

Итак это целая эпопея. Попробую покороче, но вряд ли получится.
Сначала я уяснил, что моя схема гистерезиса работает совершенно не по тому алгоритму, который я приводил выше. У этой схемы алгоритм работы гораздо проще. Начал изобретать новую схему, работающую именно по задуманному алгоритму. Изобретал - изобретал, схема разрослась до неприличия, но не работала. И тут меня осенило! Спрашивается, а нахуа? Ведь чем плоха эта схема? А плоха она тем, что переключения идут не на каждую единицу, а перескакивают через несколько единиц. Например, если гистерезис стоит +4/-4, то наше число (макс. 1023) будет увеличиваться/уменьшаться четверками. Сколько ступенек получается? А получается 1024/4=256 ступенек. А сколько нам ступенек надо? А надо нам 64 ступеньки. А это значит, что если мы поставим гистерезис +16/-16, то мы как раз и получим 1024/16=64 ступеньки. Таким образом +16/-16 это критический гистерезис. Поставим ниже, промежуточные значения все равно пропадут впустую. Поставим выше - будут потери в количестве ступенек.
Итак, ставим гистерезис +16/-16 и не паримся !!!!!!!!!!!!!!! А это ого-го, какой большой гистерезис!!! Представляете, какой должна быть помеха, чтобы попасть в такой диапазон!
Ну а дальше все тоже самое.
Вот вы Юрий в своей схеме сделали почти также, но немного по-другому. Вы сначала диапазон поделили на 16 (эквивалент сдвигу на 4), а потом сделали гистерезис +1/-1. Больше уже сделать нельзя, это приведет к потерям.
Я приведу свою окончательную схему.

Не могу сказать, чья схема лучше с точки зрения нечувствительности к помехам. Вроде одинаково должно быть. А может и нет. Что-то мне интуиция подсказывает, что моя расстановка более помехоустойчива...
А скажите, вы пришли к своей схеме эмпирически или тоже расчетом?
Я поставил ReadBackи в целочисленном формате 32.0. Все прекрасно видно. ReadBack после блока сдвига четко пробегает все числа от 0 и до 63.

И еще. У меня Index Lookup Table стоит стандартный. Видите на нем 2 точки зеленая и синяя. Можно переключать форматы ввода и вывода. У меня формат ввода стоит целочисленный 32.0. Просто представление более привычное и легко отслеживаемое.

 

[uriy]

А скажите, вы пришли к своей схеме эмпирически или тоже расчетом?

Вы про мою схему с НЧ фильтром или про свою схему в которой я перенёс операцию сдвига на выход АЦП?

Хотя наверно не важно, в обоих случаях я это делал в большей мере эмпирически, так сказать на глазок, или как ещё любят говорить некоторые математики - методом научного тыка. Я к расчётам прибегаю в очень крайних случаях, когда это очень важно для достижения некой конкретной цели.
Но в целом ваша затея мне понятна и мне просто было видно, что в моём случае лучше резать помеху сразу на выходе АЦП. Я в принципе понимаю что сдвиг это отбрасывание разрядов и мы этим действием отбрасываем четыре младших разряда от десяти разряов, но это нас не избавляет от "проброса" шумовой единицы в пятый разряд, когда четыре младших разряда равны единице, что в итоге и заставляет вводить некий гистерезис во всё это мероприятие.
Я не хотел увеличивать разрядность в блоке сравнения Tol т.к. это приводит к большему замораживаемому значению в крайних зонах. т.е. очень редко можно получить нуль на выходе такой схемы когда потенциометр уходит в ноль но медленно, и так как мне было лень считать насколько это важно, или не важно, я просто перекинул сдвиг разрядов на выход ЦАПа и получил очень малое выходное значение на выходе схемы при нулевом входе в АЦП.
По поводу помехоустойчивости, на вскидку вроде как очевидно то, что эти два метода эквивалентны, если на гистерезис задействовано одинаковое число разрядов, а вот какой метод более устойчив при минимальном количестве разрядов затраченных на гистерезис, я затрудняюсь сказать. Тут уже нужно считать.
В целом ваша схема на мой взгляд довольно оригинальная и проста и самоео главное - рабочая.

Видите на нем 2 точки зеленая и синяя. Можно переключать форматы ввода и вывода.

Хммм... незнал, буду знать.

 

[Rimtotal]

там в конце есть описание настройки кроссовера...

Kyiv
Спасибо большое!
Но если честно, я не понял пример настройки кроссовера с Дефоникой.
Я немного знаком с ней, просто под Виндовс 10 у меня не хочет она корректно работать.
Ну так вот, насколько я понял дефоника вполне самодостаточная прога, сама может раскладывает на каналы и отдает на указные выходы, виртуальный кабель ей зачем?
Я правильно понимаю что ВАК самостоятельно не умеет работать с VST плагинами?

 

[Zandy]

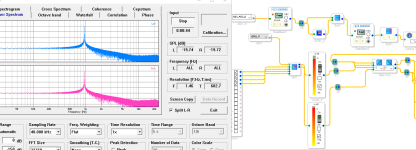
Юрий, а хотите удивлю еще разок? Вот смотрите:

Обратите внимание на то, что стоит между гистерезисом и AUX_ADC. А стоит там своеобразный фильтр, который называют субтрактивным фильтром! Ни один из библиотечных фильтров не работает корректно, а этот работает!
Блок DCB1 - отсекатель постоянной составляющей. Почему-то его не называют ФВЧ, хотя он вроде таковым должен являться. Так вот, из смеси постоянной составляющей и переменного шума помехи мы вычитаем переменный шум помехи и... вуаля... остается чистая постоянная составляющая без помехи! В эквиваленте получаем субтрактивный ФНЧ. И что самое интересное, эта хрень работает!!! Первый ридбэк мельтешит младшим разрядом. А второй - стоит, как вкопанный! Причем постоянная составляющая передается без искажений.

 

[uriy]

Юрий, а хотите удивлю еще разок? Вот смотрите:

Да, удивили.
Весьма оригинальное решение, и аудиофилов можно завлекать - АЦП с субтрактивнйо фильтрацией обеспечивает максимально качественную регулировку громкости без вращения фазы.

Завтра проверю её в железе, если инерция на регулировку громкости у схемы умеренная, и шум будет подавлен, то это пожалуй будет самой простой схемой борьбы с шумом на выходе АЦП.

Решил я не ждать, больно заманчивая схема.
В общем облом с этим подходом, при моём уровне шума на входе АЦП появляется узкое место как раз на числе 623=1001101111 что явно указывает на "проброс" шумовой единицы выше 4 разряда, даже при шуме 1 младший бит.
А так в целом схема отзывчивая на регулирование громкости, но к сожалению инерции которую должен давать блокиратор постоянки, недостаточно что бы сгладить шум полностью.
Я кстати у себя вижу дребезг младшего разряда до и после субтрактивной фильтрации. С АЦП я вижу диапазон чисел 624-622 после фильтрации крайне редко виден дребезг 623-624. Хотя частота и уровень дребезга после фильтрации меньше и реже, но он есть.

 

[Zandy]

В общем облом с этим подходом, при моём уровне шума на входе АЦП появляется узкое место как раз на числе 623=1001101111 что явно указывает на "проброс" шумовой единицы выше 4 разряда, даже при шуме 1 младший бит.

Я ведь и раньше говорил, что фильтр в принципе не должен спасать от пораженных точек. Как ни фильтруй, они все равно должны оставаться, просто количество их падает. Поэтому тот фильтр, который вы "нащупали" заслуживает отдельного внимания. Вместе с некорректностью в работе мы бонусом получаем отсутствие пораженных точек, что я никак не могу объяснить.
_____________________________________
Кстати, вы обратили внимание, что в схеме, которую я привел, гистерезис я не стал удалять. Я просто добавил этот фильтр для повышения помехозащищенности.

 

[uriy]

Я ведь и раньше говорил, что фильтр в принципе не должен спасать от пораженных точек.

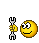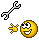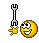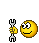
Не вижу причин по которым ФНЧ не должен убирать шум в не послы его пропускания. По этому я и применил срез ФНЧ в 3Гц, что бы шум выше 3Гц был подавлен, что в итоге и убирает "дребезг" разрядов который происходит с частотой выше частоты среза фильтра, но при этом я получаю большую инерцию по отношению к вашему варианту на гистерезисе.

Рассматривайте "поражённые точки" как шум определённой амплитуды и частоты, шум который складывается с постоянной составляющей, и тогда у вас всё сложится в голове. Шум у нас распространяется на весь спектр частот, но его уровень в диапазоне частот 0-3ГЦ ничтожно мал, а всё что выше 3Гц, шум подавляется ФНЧ и он не пропускает его на свой выход. Вот и всё, не суть важно как далеко пробрасывается шумовая единица на выходе АЦП, суть важно это частота этого процесса т.е. спектральное распределение шума, это важно если применять ФНЧ.

Я просто добавил этот фильтр для повышения помехозащищенности.

Мне кажется это излишняя перестраховка, ваш гистерезис вполне хорошо справляется с блокированием проникновения шума в тракт.

 

[Zandy]

но его уровень в диапазоне частот 0-3ГЦ ничтожно мал

Когда мы имеем дело с цифровой интерпретацией аналогового сигнала, уровень всегда определяется разрядностью его представления. Я сейчас про амплитуду, а не про спектральную плотность!
Я все понимаю, что вы говорите, а вы почему-то не хотите понять меня. Еще раз. Ни один фильтр, даже самый суперпуперский не избавит вас от шумов квантования! Фильтрация - это линейное преобразование, работающее во временной области. Этот шум квантования, амплитуда которого изначально в идеале равна 1/1024 при 10 битном АЦП, при отсекании разрядов (тем или иным способом) пролезает в любой разряд. Даже, если мы отсечем 9 младших разрядов и оставим всего 1 (!) разряд, все равно он будет там присутствовать. Но это будет всего одна пораженная точка на весь диапазон. Она будет ровно посередине диапазона. В нашем случае, где мы делим весь диапазон на 64 ступеньки по 1 дб на каждую ступеньку, дребезг в пораженных точках, вызванный шумом квантования, будет с амплитудой коэффициента передачи в 1 дб. Другими словами, это будет модуляция усиления в 1 дБ. Конечно, можно сказать, что мы не услышим такую модуляцию, точно также, как мы не слышим 0.1% THD, но тут мы уже вторгаемся в область субъективного...
Теперь о частотной полосе среза. Представьте тональный сигнал, например 1000Гц. Замодулируем его амплитуду в 1 дБ с частотой 3Гц. Неужели вы этого не услышите?
__________________________
Понимаете, я сейчас говорю не про помеху. Помеху, да, вы отфильтруете. А шум квантования никогда! Вы только сместите его в другую частотную область. Конечно, пораженных точек может быть немного, допустим только 2-4 на весь диапазон, при хорошем раскладе может их вообще не быть. Я сейчас не готов сказать, как определить количество этих точек. Но... вероятность нарваться на такую точку при регулировке по закону бутерброда всегда есть. И тут спасает только гистерезис, или введение зоны нечувствительности (нелинейное преобразование). Да, при регулировке появляется неопределенность в 1 шаг регулирования, но при этом будет отсутствовать дребезг этого шага в процессе работы.

 

[uriy]

Ни один фильтр, даже самый суперпуперский не избавит вас от шумов квантования!

А он и не должен нас избавлять от шума полностью, он подавляет шум т.е. уменьшает его уровень на величину согласно своих свойств.

Теперь, если мы возьмём узкополосный полосовой фильтр с полосой пропускания 1Гц, то уровень шума на выходе этого фильтра во всей полосе частот значительно уменьшится т.к. шум распределён по частотной шкале, а полосовой фильтр пропускает сигнала только в полосе 1Гц т.е. всё что выше и ниже частоты настройки фильтра, подавляется этим фильтром. Это касается и шумов квантования, как явный и простой пример смотрите на мои спектрограммы, уровень полки шума на них находится на уровне -130дБ при реальном уровне полки шума на уровне -96дБ т.к. сам принцип спектрографа это фильтрация сигнала в узкой после частот т.е. подавление всего и вся что не входит в измеряемую частоту. По этому шум проникающий в полосу измерения спектрометра всегда ниже чем на самом деле, и шум будет тем ниже, чем уже полоса пропускания спектрографа которая в свою очередь зависит от величины окна - FFT Size.

Теперь о частотной полосе среза. Представьте тональный сигнал, например 1000Гц. Замодулируем его амплитуду в 1 дБ с частотой 3Гц. Неужели вы этого не услышите?

Вы не хотите понять что ФНЧ не позволяет произойти этому событию т.к. уровень шума в полосе частот 0-3Гц ничтожно мал, так мал, что на выходе фильтра мы всегда видим одно число, без дребезга разрядов.

Помеху, да, вы отфильтруете. А шум квантования никогда!

Шумы квантования фильтруются ФНЧ ровно так же, как и просто шумы. Уменьшение полосы пропускания частот всегда приводит к уменьшению уровня шума в этой уменьшенной полосе частот.

З.Ы.
Что бы не попасть в дебри отраженных частот и наложения спектров и не запутаться там, стоит оговорить, что рассматривайте всё казанное мною как о диапазоне звуковых частот при минимальной частоте дискретизации сигнала в 40кГц. Т.е. оцифрованный сигнал удовлетворяет критерию Найквиста-Шеннона.

 

[Zandy]

Для меня,то что измеряет спектрометр, загадка загадочная. Вы же измеряете шум основного канала, а не канала регулирования. Шумы двух каналов перемножаются, а не складываются! Шум канала регулирования мультипликативен, а не аддитивен. Другими словами, шум канала регулирования должен проявляться во всей своей красе при наличии сигнала в основном канале. Если сигнал в основном канале равен нулю, то и шум канала регулирования не должен никак влиять. Поэтому я сразу принял эту спектрограмму за чудеса именно цифровой обработки. Мы толком не знаем, что и как там делается. Функциональная, по сути схема, которую мы рисуем, может не отражать реальную. Подходить с аналоговыми мерками, думаю, не совсем правильно.

Вы не хотите понять что ФНЧ не позволяет произойти этому событию т.к. уровень шума в полосе частот 0-3Гц ничтожно мал, так мал, что на выходе фильтра мы всегда видим одно число, без дребезга разрядов.

Я хочу вас понять, но не понимаю. О каком уровне шума вы говорите? Об амплитудном? Так амплитуда этого шума всегда будет равна величине младшего разряда. О спектральной плотности? Да, действительно, спектральная плотность в полосе 0-3Гц гораздо меньше, чем во всей полосе. Но что с того? Просто после ФНЧ полоса частот, в которой происходит дребезг, сместится в более низкочастотную область и упадет его спектральная плотность. Но амплитуда этого дребезга не поменяется, т. к. она зависит только от разрядности ЦАПа! И меньше младшего разряда просто физически не может быть.

 

[Zandy]

уровень шума в полосе частот 0-3Гц ничтожно мал, так мал, что на выходе фильтра мы всегда видим одно число, без дребезга разрядов.

Давайте на конкретном примере. Задам провокационный вопрос. На входе фильтра мы наблюдаем шум квантования. Положим число меняется 345...346. Если вы говорите, что на выходе фильтра будет одно число, то какое, 345 или 346?

 

[uriy]

Просто после ФНЧ полоса частот, в которой происходит дребезг, сместится в более низкочастотную область и упадет его спектральная плотность. Но амплитуда этого дребезга не поменяется, т. к. она зависит только от разрядности ЦАПа! И меньше младшего разряда просто физически не может быть.

Если у вас амплитуда дребезга на выходе ФНЯ не меняется, то это не ФНЧ. Я в принципе понимаю вашу позицию и считаю её не верной, но простыми словами показать её не верность не могу.

На входе фильтра мы наблюдаем шум квантования. Положим число меняется 345...346. Если вы говорите, что на выходе фильтра будет одно число, то какое, 345 или 346?

Пожалуй это самый простой путь показать что на выходе фильтра будет константа без дребезга разрядов.
Я применю самый простой фильтр НЧ, я найду среднеарифметическое этих двух значений. т.е. на воде фильтра у меня идёт последовательность из чисел 345 346 345 346, я беру два значения которые идут друг за другом и нахожу среднее арифметическое. c=(a+b)/2
а=345
b=346
c=(a+b)>>1
a+b=345+346=101011001+101011010=1010110011
После деления на два т.е. после сдвига числа вправо на один разряд, мы получаем ответ.
с=101011001=345.
Вот и всё, на выходе моего простого фильтра будет число 345 у которого не дребезжит младший разряд при любой длительности поступления на вход данной последовательности.

 

[Zandy]

Если у вас амплитуда дребезга на выходе ФНЯ не меняется, то это не ФНЧ. Я в принципе понимаю вашу позицию и считаю её не верной, но простыми словами показать её не верность не могу.


Пожалуй это самый простой путь показать что на выходе фильтра будет константа без дребезга разрядов.
Я применю самый простой фильтр НЧ, я найду среднеарифметическое этих двух значений. т.е. на воде фильтра у меня идёт последовательность из чисел 345 346 345 346, я беру два значения которые идут друг за другом и нахожу среднее арифметическое. c=(a+b)/2
а=345
b=346
c=(a+b)>>1
a+b=345+346=101011001+101011010=1010110011
После деления на два т.е. после сдвига числа вправо на один разряд, мы получаем ответ.
с=101011001=345.
Вот и всё, на выходе моего простого фильтра будет число 345 у которого не дребезжит младший разряд при любой длительности поступления на вход данной последовательности.

Да, согласен с вами. Я тут немного заблуждался. Может вы объясните механизм возникновения пораженных точек, а то я тоже этого не сильно понимаю. Почему я так настаивал на своей позиции? Практика! Туды ж ее в качель! Я уже говорил, что делал как-то регулятор громкости не на ADAU а на простом микроконтроллере. Так вот, там я применял фильтрацию по алгоритму "скользящее среднее", как самому простому в реализации. Объявлял массив из 8 элементов. В бесконечном цикле записывал туда свежие отсчеты с АЦП, инкрементируя индекс массива по кругу. В каждом проходе суммировал все элементы массива и сдвигал результат вправо на 3 бита. Использовал результат для регулятора громкости (передавал по I2C). Я конечно нисколечко не программист (просто работаю рядом с программистами ), но вроде все делал правильно. И полностью от дребезга с помощью такой фильтрации отделаться не смог. Поэтому и применил гистерезис, который сразу решил проблему.

 

[uriy]

Может вы объясните механизм возникновения пораженных точек, а то я тоже этого не сильно понимаю.

Как можно объяснить то, чего нету?

В потоке данных которые идут с АЦП нету поражённых точек, там банально идёт поток данных с шумом.

У нас есть шум в сигнале, у этого шума есть своя амплитуда и частотная плотность. Когда мы делаем выборку сигнала с частотой 48кГц то мы видим проявление этого шума как "дребезг разрядов", при оцифровке к внешнему шуму поступающему на вход АЦП так же прибавляется шум квантования, фазовый шум задающего генератора так званный джиттер и т.д. и т.п. в общем на выходе АЦП мы видим суммарное воздействие всех возможных шумов которые проникают в полезный оцифрованный сигнал. Я описываю упрощённо т.к. на самом деле там происходит модуляция шума с полезным сигналом, но это больше запутывает чем показывает некую суть. В общем, далее следует вспомнить что сдвиг разрядов в двоичном числе это операция деления, а операция деления не может уменьшить плотность шума в определенном частотной области т.е .операция деления не может выполнять интегрирующую функцию т.е. делением нельзя сделать фильтрацию сигнала. Среднеарифметическое это тоже, не совсем то и фильтрация, это её подобие т.е. очень грубо говоря среднеарифметическое это фильтр первого порядка с высокой частотой среза т.е. такой метод имеет очень слабое подавление шума в сигнале т.к. имеет большую полосу пропускания и малое подавление шума в полосе задержания.
Что бы не выворачивать себе мозги на изнанку, намного проще делать логический анализ по принципу аналоговых цепей, Найквист с Шенноом доказали то, что если частота выборки данных в два раза выше максимальной частоты в сигнале, то такой сигнал не имеет потери информации и его можно анализировать ровно так же, как и исходный аналоговый сигнал. Т.е. всё то, что распространяться на аналоговый сигнал, так же будет распространяться на его цифровое представление. Т.е. если фильтрация уменьшает плотность шума в аналоговом сигнале, то и в цифровом сигнале цифровая фильтрация будет уменьшать плотность шума в сигнале. Если делитель напряжения не обладает функцией фильтра в аналоговом мире, то и в мире цифрового отображения сигнала функция деления не обладает функцией фильтрации и т.д. и т.п.

Поймите что я тоже не обладаю спец образованием в области цифровой обработки сигналов, я просто очень давно изучал теорию связи и нам там немного и поверхностно преподавали цифровую обработку сигналов, так что мои объяснения весьма условные и требуют много оговорок т.е. на самом деле всё немного сложнее чем я описываю, но в целом я попытался передать суть почему фильтрация избавляет нас от «дребезга разрядов» в числе.

Ну и думаю не сложно понять, что чем выше уровень шума тем выше порядок ФНЧ нужен, и чем уже полоса ФНЧ тем меньше шума будет в сигнале после ФНЧ, и если уровень шума подавляется ФНЧ до величины при которой вес одного разряда числа выше этого уровня шума, то мы не увидим дребезг разряда т.к. шум ниже. Т.е. если у нас 1 бит весит 0,02В, а шум с помощью ФНЧ давится до 0,002В то у нас просто нет разрядов которые могут отобразить 0,002В т.е. мы задавили шум ниже разрешающей способности числа. Но за это мы платим уменьшением частотного диапазона сигнала, что при оцифровке постоянного напряжения не так важно, но тем не менее мы получаем серьёзную инерцию когда нам нужно подавить шум ниже плинтуса т.е. мы получаем медленное приращение громкости на выходе ЦАПа.

Ну вот как то так. Проще я не могу объяснить….

По поводу спектрографа. Он по сути является узкополосным фильтром с большой круизной среза. Спектрограф на каждой частоте спектра проверяет наличие в исходном сигнале именно той частоты на которую настроен узкополосный фильтр, и так он делает для всех частот в спектре. Само собой математика этого процесса сложнее чем я описываю, но суть именно в том, что спектрограф фильтрует сигнал в узкой полосе, тем самым уровень шума который проникает в полосу фильтрации тем ниже чем уже полоса частоты которую зондирует спектрограф. FFT size по сути является критерием полосы пропускания, чем выше число в FFT size тем уже полоса пропускания на искомой частоте, и как следствие уровень шума там меньше, именно по этому от размера FFT size зависит уровень полки шума, а настоящий шум легко рассчитывается из показаний спектрометра если знать размер окна FFT size.

Вот к примеру у меня на спектрограммах уровень полки шума -130дБ при этом FFT size равен 32768, в итоге уровень реального шума который поступает на вход спектрометра выше показаного на спектрограмме на 10log(32768/2)=42дБ.

На картинке как раз отчётливо видно что уровень всех шумов ниже теоретически достижимого если применять к сигналу фильтрацию, но уменьшая шум в частотной полосе мы теряем ширину частотной полосы.

 

[Zandy]

Отлично Юрий. Просто отлично!
Но... назрел очередной вопрос.
А как у вас обстоят дела с блоками "Probe" и "Stimulus"? Меня эта хрень жутко раздражает. То она работает, то не работает. Самое главное, непонятно, чего ей надо, чтобы она работала и какие у нее ограничения. Пляшешь, пляшешь вокруг нее, а она ни в какую. Блочки переставишь местами, глядь, она заработала. Вернешь блочки назад - опять работает. А иногда так закочевряжется, что приходится программу закрывать и заново запускать. Это что? Банальные глюки? У вас тоже так? Волшебное слово, чтобы она работала и не выпендривалась, знаете?

 

[uriy]

У вас тоже так?

Да у меня всё так же.

Волшебное слово, чтобы она работала и не выпендривалась, знаете?

Нет, не знаю.

Я просто использую пробник как можно реже, т.е. в крайнем случае, когда нужно чётко знать ответ в некой части цепи. В сигма студио есть и другие более "опасные" подводные камни, она зараза, иногда ловит глюк и никак не показывает это, и порой сидишь настраиваешь схему, сигма показывает что прошивает адау, а на самом деле ни чего она не прошивает, и вообще всё что я вижу на экране, это мираж. Я борюсь с таким проявлением глюков только режимом онлайн, т.е. внутри проекта у меня есть указатель уровня сигнала, я подаю музыку на вход адау, и смотрю наличие этого сигнала на всём протяжении создания проекта. Тем самым я имею чёткую обратную связь что сигма студио не глюкнула и общается с адау как положено. Но всё равно, даже такой подход порой не спасает от глюка в сигме. Но в целом, рано или поздно ты уже начинаешь замечать где сигма дурит тебя, и пора перегружать сигму студо или упрощать проект т.к. в нём много того, что сигму выводит из равновесия.
Ну и в целом, чем проще проект тем стабильней работает сигма студио. Благо мне нет необходимости нагружать ДСП по максимуму. Три полосы с коррекцией не требуют много ресурсов от дсп.

 

[Zandy]

Да, есть такое.
У меня вот еще неприятная штука. Иногда после перепрошивки проекта усилитель впадает в перегруз и блокируется. Причем полезного сигнала на входе вообще нет. Конечно, если я буду перепрошивать с выведенным регулятором уровня в самом усилителе на ноль, блокировки не будет происходить. Но тут конечно об усилителе - отдельная тема. В нем ведь тоже есть маленькая DSPэшечка, и я его конфигурирую от отдельного микроконтроллера. Другими словами ADAU после перепрошивки выдает на выход сигнал (по I2S), который может (не всегда) перегружать и блокировать усилитель. На слух это проявляется как громкий "Ба-бах". Я даже опасаюсь за динамики. Хорошо бы придумать какую-нибудь задержечку, вывести с ADAU какой-то сигнальчик, который бы запирал усилитель на время прошивки и чуть дольше.

 

[uriy]

На слух это проявляется как громкий "Ба-бах". Я даже опасаюсь за динамики. Хорошо бы придумать какую-нибудь задержечку, вывести с ADAU какой-то сигнальчик, который бы запирал усилитель на время прошивки и чуть дольше.

Ну очевидно что во время прошивки, адау может чудить на своих выходах всякое, и тут самое очевидное решение это блокировать усилитель с помощью детектирования клока на пине SCL, это можно сделать с помощью МК, а можно сделать с помощью RC цепочки и транзистора, завязав их на вход блокирования работы чипа усилителя, муте или ресет.
У меня в силовом ЦАПе хлопки при перепрошивке адау происходят весьма редко, но если происходят, то это звучит весьма громко т.к. 100Вт на канал это не шутки, особенно когда у моего дежурного динамика чуйка под 100дБ, мне на нём удобно отслеживать уровень шума на выходе ЦАПа. Раньше я настраивал ЦАП при питании 12В, тем самым перегруз ЦАПа не приводит к уж сильно громким хлопкам, я пользователям моего ЦАПа рекомендую настраивать программу в адау при 12В питании ЦАПа, тем самым они защищают динамик от разных ошибок в сигма студио и т.д. и т.п. А уж когда они определились с нужными настройками в сигма студио, тогда уходить на 32В питание и гонять активную АС в хвост и гриву.

 

[Zandy]

и тут самое очевидное решение это блокировать усилитель с помощью детектирования клока на пине SCL, это можно сделать с помощью МК, а можно сделать с помощью RC цепочки и транзистора, завязав их на вход блокирования работы чипа усилителя, муте или ресет.

Какой SCL вы имеете ввиду? Который в SPI программатора USBi? Не годится. Мы же через него не только программируем, но и управляем процессом в реальном времени. Надо как -то использовать сигналы протокола I2S. Тут тоже, MCLK наверное идет с ADAU непрерывно, от него мало толка. Вот BCLK, не знаю, прерывается во время программирования или нет? Надо осциллографом потыркаться. Если прерывается, то можно при его пропадании глушить усилитель, а при появлении таймировать 0.5-1сек. и разрешать усилитель. А если не прерывается, тогда не знаю, что еще можно сделать. Кстати в даташите на усилитель написано, что енейбл включать только после появления клока. Правда не помню, мастер-клока или BCLK.
Кстати... у меня и при переключении входов тоже пощелкивает. 3 входа: аналог, спдиф, блютуз. Аналог - стоит АЦП бесхитростный. Бдютуз выдает сразу цифру I2S. Переключаются через мультиплексор, работающий от АЦП с табличным массивом на 3 индекса. Может тут средствами сигмастудио как-то глушить. Но тут надо блокировать предваряя переключение, т. е. использовать задержки посредством таймера. Надо обмозговать. Вроде там есть еще плавное мультиплексирование. Если схемку соображу, выложу здесь.

 

[uriy]

Не годится. Мы же через него не только программируем, но и управляем процессом в реальном времени.

Да не годится. Не учёл я режим мониторинга....

Вот BCLK, не знаю, прерывается во время программирования или нет?

Не знаю, у меня выход I2S с адау в слейве используется.

 

[Zandy]

Не знаю, у меня выход I2S с адау в слейве используется.

У меня адау мастер. Все клоки он задает.
Только сейчас посмотрел осциллографом. Облом! Что MCLK, что BCLK, что LRCLK стоят, как вкопанные во время прошивки, не прерываются. DATA0 и DATA1 что-то в них меняется, какие-то пропуски наблюдаются, но что с этого поиметь, непонятно.
Может все-таки что-то в сигма студио задействовать надо, чтобы не сразу выход подключался? Какую-нибудь задержку организовать...? Конечно, прошивка - событие редкое, защита в усилителе срабатывает, если ручка громкости повернута больше половины. Может и хрен с ним, со щелчком...? Там защита интегрирована сразу от многих событий. Есть регистр ошибок, который можно вычитывать и определять какое событие вызвало срабатывание защиты. Но... к сожалению, я эту возможность не задействовал. А можно было микроконтроллер соединить по UARTу с компом, с какой-нибудь терминальной программой. На работе от меня потребовали бы в приказном порядке. А тут для себя... вольный художник. А-а-а, и так сойдет...

 

[uriy]

Может и хрен с ним, со щелчком...?

Может все-таки что-то в сигма студио задействовать надо, чтобы не сразу выход подключался? Какую-нибудь задержку организовать...?

В момент прошивки в адау ни чего не работает как я понимаю. Вообще что бы поймать момент прошивки можно мониторить I2C порт с помощью МК и отлавливать команду на прошивку адау т.к. эта команда специфическая, но это в каком то смысле головоняк, легче подзабить.

 

[Zandy]

Что-то меня тюкнуло в голову... А вдруг адау после перепрошивки постоянный уровень выдает, по нему и защита в усилке срабатывает? Надо на выход попробовать блочок отсекания постоянки поставить. А вдруг...?
Кстати, смотрел чужие проекты, так там этих блочков немерено. Не понимаю, зачем? Правда структуру не анализировал. Может там какие-нибудь нелинейные преобразования? Или просто, на всякий случай?

 

[uriy]

Надо на выход попробовать блочок отсекания постоянки поставить. А вдруг...?

 

[Zandy]

Давно я тут не был. Ковид скосил. Думал, что уже нет его, оказывается живет и здравствует. Просто перешел в разряд рядового гриппа.
Так вот, проблема успешно решена. Подсказали на форуме чипа с дипом. Мне даже жутко стыдно стало, что я сам до такой ерунды не додумался. А решение - вот оно:

На дискретный выход DSP подается простой лог. уровень 1. Когда мы прошивем DSP, на этом выводе лог. 0. После прошивки там опять лог. 1. Ну а дальше как кому нравится. Я сделал так:

Это конфигурационный МК, который рулит функциями усилителя. Сигнал TEST_WORK это тот самый сигнал с DSP. В DSP он должен быть сконфигурирован, как выход без внутренней подтяжки, т. к. питания разные.
Ну и добавлены несколько строчек кода в главном цикле:

Вот так все оказалось примитивно. Все прекрасно работает. В защиту усилитель не переходит, щелчков в динамиках нет.

 

[uriy]

Мне даже жутко стыдно стало, что я сам до такой ерунды не додумался.

Что бы до этого додуматься, нужно знать что адау в момент прошивки держит свои порты в нуле, т.к. это не очевидно, у разных микросхем это по разному.