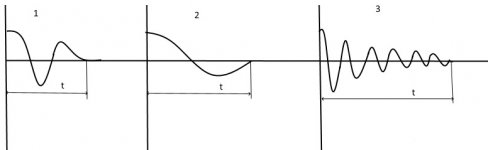
Не знаю, к месту или нет, в инстике преподавали механические системы регулирования, не совсем полагаюсь на память, но главное было в них вернуть состояние после внешнего воздействия как можно быстрее и точнее, либо занять новое состояние с такой же скоростью и точностью. От руки набросал графики законов, которые делали это быстрее и точнее. Нарисовано криво, но суть понятна, лучший график номер 1, реакция с быстрым затуханием, с однократным небольшим заходом в сторону воздействия. График 2 и 3 не позволяет достигнуть точности за короткое время. Громкоговоритель это механическая система которая возвращает свое состояние при снятии воздействия, возможно его правильная конструкция и материалы позволят осуществить "правильный" переходный процесс, обеспечить его звучность и микродинамику.
Уважаемый fishrob, Вы справедливо и к месту напомнили эти классические переходные процессы в системах регулирования. Об этом уже писал "Просто Коля" в одной из веток на данном форуме (
https://ldsound.club/index.php?threads/yamaha-ns-6490.1014/page-4) в сообщении #99 и моём ответе на него в #104.
Действительно, если Вам необходимо реализовать максимальное быстродействие системы в её реакции на ступенчатое входное воздействие, то оптимальным по быстродействию переходным процессом будет переходный процесс с допустимым небольшим забросом выше "полки" отрабатываемого входного сигнала не более, чем на 5-8% (от значения "полки") с одним растянутым периодом заброса и его апериодическим выходом на саму "полку". Если продолжить и далее увеличивать быстродействие (за счёт увеличения коэффициента сквозного усиления системы), то получим своеобразный затухающий по амплитуде колебаний "звон" из многих колебаний, что в большинстве случаев механических систем недопустимо либо из соображений механической прочности объекта , либо, повышенных искажений звука в АС из-за этих отсутствующих в исходной входном сигнале переходных свободных колебаний объекта управления.
Вышеописанный оптимальный "одноколебательный" переходный процесс осуществляется подбором оптимального соотношения значений двух коэффициентов усиления в системе: коэффициента усиления входного сигнала (Ку) и коэффициента демпфирования (Кд), умножаемого на скорость перемещения объекта управления и приводящему к демпфированию (затуханию по амплитуде) его свободных (паразитных) колебаний, вызванных проявлением свойства инерции управляемого объекта (его массы, например, массы подвижной части динамика).
Наблюдая ход данной дискуссии о "микродинамике" АС при условии наличия больших уровней составляющих в общем входном сигнале прихожу к выводу, что аргументированно ответить на данный вопрос удастся, видимо, только с применением двух подходов: реальных измерений и моделирования:
1. Реальное измерения на АС с применением измерительного микрофона для записи звукового сигнала, представляющего из себя сумму двух синусоид большой и малой амплитуд с разными частотами, отличающимися в несколько раз и дальнейшим измерением соотношения амплитуд двух составляющих сигнала от микрофона, например, при просмотре записанного сигнала от микрофона на экране осциллографе, как это сделал М.М. Эфрусси в своей книге "Громкоговорители и их применение" от 1976г на рис.15 стр.27., скриншот с которого и привожу ниже. К сожалению, приведенной информации маловато, чтобы сделать уверенный вывод о наличии эффекта "динамического экспандирования в динамиках", хотя намёки на это уже заметны на рис.15 даже при наличии на некоторых рис. эффекта от выхода катушки динамика из рабочей области действия магнита динамика.
Кстати, к вопросу о непрерывном "прогрессе" измерительного инструментария: за прошедшие с момента публикации почти пол-столетия ничего подобного найти в Интернете мне не удалось, одно болтовня. А как казалось бы, не так уж и сложно провести такие измерения при наличии микрофона и современного осциллографа.
2. Моделирование колебаний диафрагмы на простейшей модели динамика с учётом действия трёх основных сил возбуждающей силы от тока в катушке динамика, демпфирующей силы от центрирующей шайбы динамика и силы аэродинамического сопротивления воздуха движению диафрагмы с учётом массы подвижной части динамика. Довольно простая задачка сводится в двойному интегрированию по времени текущего ускорения катушки динамика с целью получения скорости и амплитуды колебаний катушки по времени.
А поскольку способности нашего мозга в двойном интегрировании весьма ограничены, то все словопрения без проведения эксперимента или его моделирования ни к чему существенному не приведут (пример тому вышеприведенный разбор "взрыва в космосе"). Однако, "раз пошла такая пьянка", то возьму на себя обязательство провести моделирование движения катушки динамика по 2 пункту на ПК и тем самым проверить свою вышеизложенную (и дружно проигнорированную сообществом) версию "динамического экспандирования в динамиках". Думаю, на это мне понадобится не более месяца, поскольку не программировал уже пару лет, а этот процесс требует, как и у музыкантов, периодической тренировки.
P.S. Кстати, зря тут некоторые игнорируют важнейшую роль аэродинамического сопротивления воздуха движению диффузора, которая пропорциональна квадрату скорости его движения, а при условии постоянства амплитуды колебаний диффузора ускорение диффузора пропорционально квадрату частоты сигнала, а скорость диффузора пропорциональна частоте сигнала. Из этого следует, что сила аэродинамического сопротивления (с учётом её квадратичной зависимости от скорости) пропорциональна квадрату частоты сигнала (опять же, при условии постоянства амплитуды колебаний).
Для примера, раскройте зонтик и попробуйте за его ручку начать постепенно начать увеличивать частоту колебаний при небольшой амплитуде колебаний (в десяток сантиметров) и прикиньте на каких всего нескольких Герцах колебаний зонтик потеряет свою форму и вывернется в другую сторону, кстати, как и диафрагма динамика, начиная с некоторой высокой частоты воспроизводимого сигнала, зависящей от жёсткости формы диффузора. Претензии о сломанном зонтике не принимаются, поскольку "предупреждён - значит вооружён".
Georgi, 3.03.2022г, 12ч 35м
3