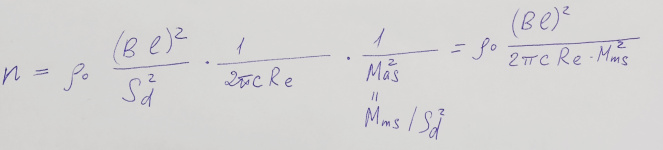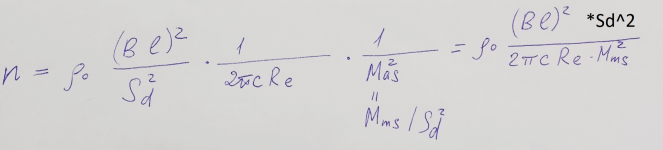НЕТ !
Вспомните эту тему когда Николай представит статью о ПАС .
Пока что я могу ответить лишь на эмоциях .
За потоки и особенно за аэродинамику о которых большинство 0 целых и пару с гугл поиска "десятых"
Ой, дорогой, не зарекайтесь! И никогда не говорите НЕТ! Кажется был такой фильм с похожим названием.
Чем больше человек знает, тем менее он категоричен, больше сомневается, понимая, что истину он не знает.
Для ознакомления с принципом работы ПАС необходимо два условия: чистый платок и желание провести эксперимент.
Для начала натяните платок в один слой и попытайтесь продуть туда-обратно воздух через него. Заметили некоторое неудобство в трудности дыхания? НЕТ? Тогда сложите платок в два слоя и повторите дыхательное упражнение.
И т. д. Наращивайте число слоёв платка-пока не посинеете. Тогда стоп. Вы слишком увеличили степень демпфирования ПАС и надо снизить число слоёв ткани. Или, просто ослабьте натяжение ткани и ПАС-а теперь уже нет и ткань просто трепыхается вместе с воздухом, не оказывая его движению никакого сопротивления.
Кстати на свойства ПАС влияет тип плетения ткани (слабое или плотное) и число слоёв ткани. Лучше всего, конечно, один слой, чтобы его можно было хорошо натянуть и не забыть установить две, перфорированные крупными соосными отверстиями, перегородки с двух сторон от ткани для предотвращения её от дополнительного трепыхания.
P.S. А аэродинамика не так и уж сложна, как вы тут говорите. По поводу расчёта силы лобового сопротивления Вы все уже полные специалисты. Формула известна. Осталось найти подходящее для нашего тела (диффузора) и соответствующее ему значение Сх из интернета и вуаля: сила может быть посчитана. А Dimon SSSR лишь слегка "попужал" всякими сложностями, которые в нашем случае для движения динамика вовсе не имеют места быть. А так всё просто как пареная репа на Руси.
Всё. На этом абзац. Пора браться за
Вильяма Шекспира , за моделирование. Обещал - надо исполнять. И посевная на носу, как и у Олега, тогда не до общения будет и не до фильтров.
А всё-таки весьма интересно. что у меня получится. Есть ли оно это экспандирование у динамика, али его нет. Нутром чую, что есть. Все признаки, отмеченные А. Бокаревым, чётко указывают на его наличие. Осталось только доказать цифрами и понять всю глубину
морального дополнительного падения малого сигнала динамика в присутствии большого. Кстати, попробую смоделировать и картинки осциллограмм рис. из книги Эфрусси. Однако, до свидания.
Georgi, 06.04.2022, 21ч. 30м.
Давление создается благодаря динамическому взаимодействию составляющих среды распространения. В основе лежит все тоже самое уравнение F=m*a из второго закона Ньютона. Просто исходя из свойств среды: упругости, плотности, сплошности и т.д. и из-за трехмерности задачи это простое уравнения трансформируется в сложные дифференциально интегральные формы.
Если же рассмотреть простейший случай плоских волн(одномерная задача, вполне реальная впрочем: пистофон, например), тогда можно ограничиться вторым законом для элементарного объема среды. Все равно получатся дифференциальные уравнения, но их вид из-за одномерной задачи будет понятен большинству окружающих, кто получил общее среднее. Попутно смысл происходящих процессов становится предельно ясен. Сходу из одномерной задачи получается, что давление порождается скоростью частиц среды и коэффициент пропорциональности между ними равен плотности*скорость звука.
Основная зависимость между параметрами среды(давление , скорость) выглядит так P=r*c* u, этот коэффициент r*c назван сопротивлением в честь и по аналогии с электрическими цепями. Поскольку зависимость напоминает закон Ома U=I*R. Скорость частиц среды - аналог силы тока(движение), давление - аналог напряжения(скалярный потенциал).
Из этого основного уравнения пошло/поехало. Интенсивность есть давление на скорость, I=P*u или I=P^2/(r*c) это понятно. Но, в ступор вводят выражения типа I=r*c*|u|^2/2. Хотя последнее тоже самое, что и P^2*u, еще взято эффективное действующее значение(/2). Что самое интересное по данному выражению можно связать скорость частиц среды в любой точке с интенсивностью волны, причем так уж получилось, что для для любого случая и двумерного, и трехмерного вид уравнения не меняется принципиально.
Дальше больше, но так же все понятно и не сложно.
Касаемо пистофона давление звуковой волны рассчитывается просто. В большинстве задач физики предполагается основной принцип непрерывности температуры и равенства скоростей на границе раздела сред. Поэтому скорость частиц среды вблизи поверхности будет эквивалентно равна самой скорости поверхности поршня(так изначально создается давление).
Исходя из этого давление развиваемое пистофоном определится простой формулой P=r*c*u, где u - скорость поршня. При условии наличия волнового процесса. Самое интересное, что сопротивление в случае плоской волны чисто активное.
В случае цилиндрической или сферической волны уравнение для для давления такое же - P=Z*u. Только здесь сопротивление излучению становится комплексной величиной, но все одно в него входит множитель r*c и различные безразмерные функции связанные с частотой, расстоянием до источника и углом.
В общем случае для поршня в бесконечном экране Pзв = ρ*с*A*ω*sqrt( (rR)2 + (xR)2 ), скорость здесь A*ω , где А амплитуда поршня, w - угловая частота, r*c - уже известный всем коэффициент, ну и корень из суммы квадратов активной и реактивной части безразмерных функций сопротивления.
Уважаемый Сергей ДВ, не надо вводить народ в заблуждение принципом работы пистонфона, создающим конкретное высокоточное значение акустического давления в ЗАМКНУТОМ ОБЪЁМЕ камеры для тарирования им показаний измерительного микрофона (см. его описание по ссылке
https://uz.denemetr.com/docs/769/index-84303-1.html?page=10)
Приведу выдержку описания работы пистонфона:
"
Пистонфон представляет собой толстостенную камеру объемом V0 (с номинальными объемами 1000, 200 и 10 см3)...
В камере перемещается по гармоническому закону с амплитудой Xm поршень 3 площадью S, вытесняющий из объема V0 камеры 2 переменный объем, равный S·Xm. Он приводится в движение, например, кривошипным механизмом. Амплитуду колебаний поршня измеряют измерительным микроскопом.
В идеальном случае, когда стенки камеры и мембраны приемника жесткие, акустическое давление в камере Pm находят из соотношения:
Pm = γ К Р0 (S·Xm / V0 ), (4.5.1)
где γ = Ср /СV - отношение удельных теплоемкостей,
Ро - давление в камере до начала перемещения поршня ..."
Из выр. 4.5.1 следует, что изменение эталонного давления в камере по гармоническому закону полностью определяется изменением по гармоническому закону дополнительных порций воздуха, перемещаемых поршнем (dV=
S·Xm), которое будучи отнесённым к общему объёму камеры
V0 после умножения на
практически постоянный для конкретных условий текущих измерений множитель (
γ К Р0) и определяет величину эталонного давления.
Как видим, эталонное давление полностью определяется конструкцией модели прибора и почти НЕ ЗАВИСИТ ( особенно при большой длине камеры) как от частоты вращения электродвигателя и частоты гармонического движения поршня, так и ОТ СКОРОСТИ ПЕРЕМЕЩЕНИЯ ПОРШНЯ. Действительно, если условно нарушить герметичность камеры (при бесконечном значении
V0) прибор практически перестанет развивать эталонное давление, несмотря на продолжающуюся работу поршня, в полном соответствии с выр.4.5.1.
Поэтому, Ваши выражения для определения давления воздуха уже с учётом СКОРОСТИ "частиц" воздух
U , якобы вытекающие из принципа работы пистонфона, никак из него не следуют. Поскольку в идеально работающем пистонфоне эталонное давление почти не зависит от того, с какой средней линейной скоростью перемещается поршень (лишь бы он не пропускал воздух за пределы камеры), а определяется лишь величиной соотношения изменяемого поршнем объёма воздуха к полному объёму замкнутой камеры.
К сожалению, ссылка на принцип работы пистонфона оказалась, увы, неудачной.
И вообще,
совершенно непонятна причина появления скорости звука (С) в выражениях для давления на малых скоростях перемещений диффузора. Вот если её заменить на текущую скорость тогда уже будет понятнее и ближе к квадрату скорости в скоростном напоре. А линейная зависимость силы сопротивления от скорости потока возможна только в формуле Стокса при ламинарном течении воздуха и, поэтому, весьма малых линейных скоростях диффузора (менее ~ 0,01...0,1 м/с).
Однако, до свидания. Georgi, 07.04.2022 22ч.37м